A Curiosa História do Número Pi: Da Antiguidade à Era Digital

O número Pi (π) é uma das constantes matemáticas mais intrigantes e essenciais. Desde tempos antigos, ele tem fascinado matemáticos, engenheiros, e cientistas por sua infinidade e sua aplicação universal em tudo que envolve círculos e esferas. Neste artigo, vamos explorar a história rica de Pi, suas aplicações culturais e científicas, e como ele evoluiu desde os primórdios da humanidade até o cálculo moderno feito por computadores.

O Que É o Número Pi e Para Que Ele Serve?

Pi (π) é a razão entre a circunferência de um círculo e seu diâmetro. Este valor é constante para todos os círculos e resulta aproximadamente em 3,14159. Sua natureza irracional significa que suas casas decimais nunca terminam e nunca formam um padrão repetitivo.

O número Pi (π) tem sido utilizado em uma vasta gama de áreas ao longo da história, tanto em aplicações práticas do cotidiano quanto em avanços científicos e tecnológicos. Aqui estão alguns exemplos concretos e universalmente conhecidos de onde o Pi já foi aplicado:

• Cúpula da Basílica de São Pedro (Vaticano): Pi foi essencial no cálculo da circunferência e da área da cúpula, uma das mais famosas do mundo. Projetos arquitetônicos que envolvem estruturas circulares ou esféricas, como cúpulas e torres, requerem o uso de Pi para medir corretamente as proporções e garantir estabilidade.

• Grande Pirâmide de Gizé (Egito): Embora Pi não tenha sido formalmente conhecido pelos antigos egípcios, a proporção entre a circunferência da base da pirâmide e sua altura sugere uma aplicação implícita de Pi. Muitos acreditam que essa relação não foi por acaso, mesmo sem uma compreensão formal de Pi como conhecemos hoje.
• Satélites GPS: O funcionamento do GPS depende de cálculos complexos de órbitas baseados em Pi, o que permite que os satélites orbitais determinem com precisão a posição geográfica de um dispositivo em qualquer lugar da Terra.
• Ondas sonoras e eletromagnéticas: Pi aparece em várias equações na física que descrevem a propagação de ondas, como as ondas sonoras e eletromagnéticas. A fórmula para a velocidade do som, por exemplo, inclui Pi, pois descreve o comportamento das ondas circulares em diferentes meios.

Esses são apenas alguns exemplos de como Pi é utilizado em diversas áreas que afetam nosso dia a dia.

Historicamente, Pi foi calculado de diversas formas, desde aproximações geométricas até o uso de séries infinitas. Métodos simples, como o de Arquimedes , envolvem-se aproximando-se Pi inscrevendo polígonos dentro e fora de um círculo, como é mostrado neste vídeo do canal Endhyel Erben no YouTube:

No entanto, com o desenvolvimento do cálculo, novas formas de calcular Pi foram descobertas.

Uma das maneiras mais conhecidas de calcular Pi é por meio da Série de Leibniz, que aproxima Pi pela soma alternada de frações:

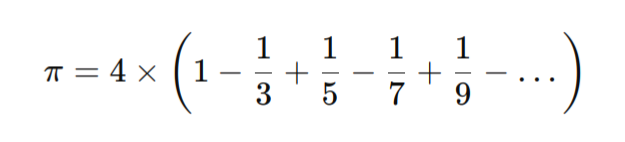
Embora essa série seja interessante, ela converge lentamente, ou seja, é preciso somar muitos termos para obter uma aproximação precisa.

O Algoritmo de Gauss-Legendre

Uma forma muito mais eficiente de calcular Pi é o Algoritmo de Gauss-Legendre , que combina conceitos de álgebra e geometria para converter rapidamente valores muito precisos de Pi. Desenvolvido por Carl Friedrich Gauss e Adrien-Marie Legendre no final do século XVIII, esse algoritmo usa uma série de cálculos repetidos entre dois números (um relacionado à média aritmética e outro à média geométrica).

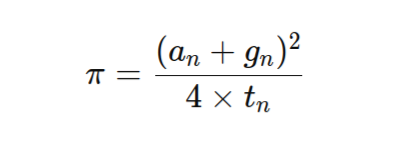
Onde:

n: Representa o número de iterações (ou passos) realizadas no algoritmo. Quanto mais iterações, mais preciso será o valor de Pi.

aₙ: Representa a média aritmética após a n-ésima iteração do algoritmo.

gₙ: Representa a média geométrica após a n-ésima iteração.

tₙ: É um valor auxiliar que vai sendo atualizado em cada iteração e ajuda no cálculo final. Ele é ajustado em cada etapa do processo para garantir que a aproximação de Pi seja precisa.

O número 4 na fórmula final do Algoritmo de Gauss-Legendre surge como parte do ajuste matemático necessário para que a aproximação de Pi seja precisa. Esse valor é uma constante que garante que o resultado final esteja na escala correta para representar o valor de Pi.

Este método é extremamente eficiente e foi uma grande revolução no cálculo de Pi. Graças a ele, Pi foi calculando com milhões de dígitos usando menos operações do que os métodos anteriores. Hoje, o Algoritmo de Gauss-Legendre é uma das principais ferramentas utilizadas por computadores para calcular Pi com uma precisão altíssima.

As Origens Antigas de Pi

O número Pi tem suas raízes na história antiga, quando civilizações como os egípcios e babilônios começaram a observar as relações geométricas entre o diâmetro e a circunferência de um círculo. Os babilônios, por volta de 1900 a.C., aproximaram o valor de Pi em 3,125, um cálculo surpreendentemente preciso para a época. Enquanto isso, os egípcios, em seu famoso Papiro de Rhind, datado de cerca de 1650 a.C., também realizaram aproximações semelhantes, estabelecendo Pi como aproximadamente 3,1605.

Essas primeiras tentativas de calcular o número Pi eram essencialmente práticas, usadas em projetos de engenharia, como a construção de monumentos e templos. As grandes pirâmides, por exemplo, mostram indícios de que os egípcios já estavam familiarizados com a importância de Pi, mesmo sem uma compreensão formal do conceito.

Embora essas antigas civilizações não tivessem os métodos matemáticos avançados que temos hoje, elas lançaram as bases para os estudos posteriores sobre o número Pi. Sua busca por precisão no cálculo de áreas e volumes de figuras circulares estabeleceu Pi como uma constante fundamental na matemática, algo que as gerações futuras continuariam a explorar e refinar.

Essa busca por uma definição exata do número Pi seria o ponto de partida para muitos outros matemáticos ao longo da história, cada um contribuindo com novas fórmulas e técnicas para calcular essa constante misteriosa e infinita.

O “Símbolo” de Pi (π)

O “símbolo” que representa o Pi (π) é, na verdade, uma letra do alfabeto grego. Ela corresponde à letra “P” (ou “pi” minúsculo) no alfabeto grego. O uso de letras gregas é comum na matemática e na ciência, devido à sua longa tradição de uso em escritos acadêmicos e científicos desde a Grécia Antiga.

A letra grega Pi (π) foi adotada oficialmente em 1706 pelo matemático galês William Jones, embora já fosse utilizada de maneira não oficial por outros matemáticos. Jones escolheu a letra grega π como uma representação da palavra grega “periphéreia” (περιφέρεια), que significa “periferia” e se refere à circunferência de um círculo. Antes disso, não havia um símbolo padrão para representar o número Pi, e os matemáticos usavam várias aproximações numéricas ou letras diferentes.

O símbolo ganhou notoriedade em 1737, quando o matemático suíço Leonhard Euler adotou o π em seus trabalhos. Como Euler era uma figura altamente influente na matemática, o uso do símbolo se espalhou rapidamente e se consolidou como a notação universal para o número Pi.

Assim, o símbolo π passou a representar a constante matemática que define a razão entre a circunferência e o diâmetro de qualquer círculo, e desde então, é amplamente reconhecido e utilizado em todo o mundo.

Pi e a Matemática Grega

A civilização grega trouxe um grande avanço na compreensão matemática de Pi, especialmente através de Arquimedes de Siracusa, um dos maiores matemáticos da história. Por volta de 250 a.C., Arquimedes desenvolveu um método engenhoso para aproximar o valor de Pi, utilizando a geometria. Ele aplicou o método de exaustão, uma técnica que consistia em inscrever e circunscrever polígonos de muitos lados em torno de um círculo, calculando suas áreas. Quanto mais lados os polígonos tinham, mais próximo ele chegava do valor correto de Pi.

Arquimedes foi capaz de aproximar Pi entre 3,1408 e 3,1429, um cálculo extremamente preciso para a época. Sua abordagem matemática foi um marco no desenvolvimento de técnicas para calcular o número Pi, e seus métodos influenciariam gerações futuras. A inovação de Arquimedes se destacou pelo fato de que, ao contrário dos babilônios e egípcios, que faziam aproximações baseadas em observações, ele aplicou princípios matemáticos rigorosos para chegar a um valor mais preciso de Pi.

Além de Arquimedes, outros matemáticos gregos também contribuíram para o estudo de Pi. Hipócrates de Quios e Eudoxo de Cnido, por exemplo, exploraram conceitos que mais tarde seriam fundamentais na compreensão de Pi, especialmente no que diz respeito às áreas de figuras geométricas.

Essa fase crucial na história do número Pi, marcada pelas contribuições de Arquimedes e outros matemáticos gregos, solidificou sua importância como uma constante fundamental na matemática, dando início a um legado que se estenderia por milênios.

Pi na Idade Média e no Renascimento

Após os avanços gregos, o número Pi continuou a intrigar matemáticos durante a Idade Média e o Renascimento. Durante esse período, a matemática foi influenciada tanto pelas tradições islâmicas quanto europeias, trazendo novas descobertas e técnicas para calcular Pi com maior precisão. Na Índia, o matemático Madhava de Sangamagrama, por volta do século XIV, desenvolveu uma série infinita que aproximava Pi, marcando uma mudança fundamental na maneira como Pi era calculado. A série de Madhava permitiu que matemáticos obtivessem valores de Pi com várias casas decimais, algo revolucionário para a época.

No mundo islâmico, estudiosos como Al-Kashi também fizeram avanços importantes, refinando os métodos de aproximação de Pi, utilizando polígonos com um número crescente de lados para calcular seu valor. Al-Kashi, por exemplo, obteve uma aproximação de Pi com até 16 casas decimais, um recorde que perdurou por séculos.

Com o advento do Renascimento, o interesse por Pi foi revitalizado na Europa. Matemáticos como o italiano Fibonacci e o francês François Viète usaram novos métodos para melhorar os cálculos de Pi. Viète foi o primeiro a usar uma fórmula baseada em uma série infinita para calcular Pi na Europa, demonstrando o impacto dos avanços matemáticos orientais no pensamento europeu.

Os matemáticos do Renascimento, em especial, se beneficiaram da introdução do sistema numérico indo-arábico na Europa, o que facilitou cálculos mais precisos. A partir daí, o valor de Pi passou a ser calculado com maior exatidão, e a busca por descobrir mais casas decimais se tornou uma obsessão entre os estudiosos.

Essa fase da história do número Pi, marcada pela fusão do conhecimento islâmico, indiano e europeu, deu início a uma era de cálculos mais precisos e ao desenvolvimento de técnicas que seriam essenciais na era moderna. O número Pi continuava a crescer em importância, não apenas como uma curiosidade matemática, mas como uma ferramenta essencial em diversos campos científicos.

Pi na Era Moderna

Com a chegada da Era Moderna, o número Pi deixou de ser uma simples curiosidade matemática e passou a ser o foco de intensos estudos, especialmente com o desenvolvimento de novas ferramentas matemáticas e tecnológicas. No século XVII, o surgimento do cálculo, com Isaac Newton e Gottfried Wilhelm Leibniz, abriu caminho para métodos mais precisos de calcular Pi, usando séries infinitas. Essas séries, como a famosa Série de Leibniz, permitiram aproximar Pi com uma precisão sem precedentes, embora a convergência fosse lenta.

Foi também nessa época que o número Pi começou a ganhar as primeiras casas decimais além das aproximações rudimentares do passado. Calculando manualmente, matemáticos foram capazes de obter valores com até centenas de casas decimais, o que representava um avanço notável.

No século XX, com o advento dos computadores, o cálculo do número Pi deu um salto gigantesco. Em 1949, o computador ENIAC, um dos primeiros computadores eletrônicos de grande escala, foi capaz de calcular Pi com mais de 2 mil casas decimais em cerca de 70 horas de processamento. Esse marco foi apenas o início de uma corrida tecnológica que, ao longo das décadas, levou a cálculos com bilhões de dígitos.

O desenvolvimento de algoritmos mais eficientes, como o Algoritmo de Gauss-Legendre e as Séries de Borwein, tornou possível calcular Pi com uma precisão absurda, utilizando menos recursos computacionais. Hoje, Pi já foi calculado com mais de 31 trilhões de casas decimais, e essa busca continua, embora valores tão extensos não tenham aplicações práticas.

No entanto, o fascínio pelo número Pi vai além da matemática pura. Ele se tornou um ícone cultural, celebrado anualmente no Dia do Pi (14 de março), data que coincide com o aniversário de Albert Einstein. Pi também inspira competições para memorizar o maior número possível de casas decimais, além de aparecer frequentemente na literatura, no cinema e na música.

9 Curiosidades Interessantes sobre o Número Pi

Além de suas inúmeras aplicações e seu impacto na matemática e na cultura, o número Pi carrega consigo uma série de fatos curiosos que continuam a fascinar o mundo:

1. Pi e a Memorização Extrema
   • Memorizar os dígitos de Pi é um desafio que muitos tentam superar. O recorde atual de memorização pertence a Suresh Kumar Sharma, da Índia, que em 2015 recitou impressionantes 70.030 dígitos de Pi. Esse feito incrível levou mais de 17 horas!
2. O Pi na Bíblia?
   • Acredita-se que a Bíblia contém uma aproximação de Pi. No Livro dos Reis (1 Reis 7:23), há uma descrição de um tanque circular de bronze construído no Templo de Salomão, onde a razão entre a circunferência e o diâmetro é descrita como sendo 3. Embora não seja uma precisão matemática, muitos estudiosos interpretam isso como uma aproximação rudimentar de Pi.
3. O Pi na Natureza
   • Pi não é apenas uma abstração matemática – ele também aparece na natureza. Você pode encontrá-lo em fenômenos como a forma de ondas, o crescimento das espirais nas conchas, e até mesmo na forma do DNA, que segue uma estrutura helicoidal relacionada a Pi.
4. Pi em Eventos Globais
   • Em 2010, Google usou o poder de seu sistema de nuvem para calcular Pi com mais de 2,7 trilhões de dígitos. Isso foi feito como parte da celebração global do Dia do Pi, uma data comemorada por matemáticos e entusiastas no dia 14 de março (3/14, em referência aos primeiros dígitos de Pi).
5. Pi e a Teoria da Relatividade
   • Albert Einstein, autor da Teoria da Relatividade, não só nasceu no Dia do Pi (14 de março), mas também usou Pi em muitas de suas equações na teoria da relatividade geral. Pi está presente nas equações que descrevem a forma do espaço-tempo ao redor de grandes objetos como estrelas e buracos negros.
6. Pi é Infinito e Sem Padrões
   • O número Pi é um número irracional, o que significa que suas casas decimais nunca terminam e nunca seguem um padrão repetitivo. Até hoje, como visto anteriormente, já se calcularam trilhões de dígitos de Pi, mas nenhuma sequência de números se repete de maneira previsível, o que o torna único e fascinante.
7. O Pi na Gastronomia
   • Além de ser celebrado no Dia do Pi, muitas pessoas aproveitam a data para fazer trocadilhos e comemorar com “pie” (torta, em inglês), que soa como “Pi”. Nos Estados Unidos, o Dia do Pi é comemorado com maratonas de matemática e muitos eventos onde tortas (pies) são a estrela principal!
8. Pi na Criação de Universos Fictícios
   • Em muitas histórias de ficção científica, o número Pi é tratado como um número quase “mágico”. No livro “Contact” de Carl Sagan, a personagem principal descobre uma mensagem escondida nos dígitos de Pi, sugerindo que a constante matemática contém segredos deixados por uma inteligência superior.
9. Pi e a Música

• Pi também foi transformado em música! Matemáticos e músicos criaram composições baseadas nos dígitos de Pi, onde cada número é representado por uma nota musical. Essas obras combinam matemática e arte de maneira surpreendente, mostrando como Pi transcende disciplinas.

A jornada do número Pi, desde suas primeiras aproximações na antiguidade até os cálculos precisos com trilhões de dígitos, é uma verdadeira história de curiosidade humana e avanço científico. Muito mais do que um número em uma equação, Pi simboliza a busca por padrões e a beleza na matemática, ligando gerações de matemáticos, engenheiros e cientistas em uma busca contínua pelo conhecimento.

Seja na construção de monumentos antigos, no desenvolvimento de tecnologia moderna, ou nas competições culturais que Pi inspira, sua presença é um lembrete de que as respostas para os grandes mistérios do universo podem ser encontradas nas constantes matemáticas que nos cercam. Assim, Pi continua a fascinar e inspirar, provando que a matemática é tão infinita quanto os próprios dígitos de Pi.